特に首都圏において、中高一貫校に進学すると難関大学に進学しやすくなるという言説が存在する。井上（2001）や和田（2008）は代表的な論者であるし、大衆雑誌や中学受験案内などで、中高一貫教育のメリットの一つとして難関大学進学への優位性が挙げられることは珍しくない。それらの言説の根拠としてしばしば提示されるのは、難関大学に中高一貫校出身者が多いという事実である。確かに、たとえば東京大学の学生に占める私立中高一貫校の出身者の割合は、53.5％（国立高校の出身者を含めれば63.6％）とかなり高い*1。

しかし、難関大学に中高一貫校出身者が多いことは、中高一貫校に進学すると難関大学に進学しやすくなるという証明にならないことには注意が必要である。というのも、中高一貫の高校はそうでない高校と比べて、入学時点で高学力の生徒を選抜している傾向があり、中高一貫校進学と難関大学進学の正の相関が、入学時点での生徒の学力水準を背後要因とする、見かけ上の相関である可能性が否定できないためである。

はたして、中高一貫校に進学することで、難関大学に進学しやすくなるという関係は存在するのだろうか。本稿において実証分析を通して回答を導きたい。


２．分析手法

中高一貫校進学が難関大学進学に与える影響を計量的に見出す方法は、大きくは二つ考えられる。一つは、同一年齢層の個人を単位として、中高一貫校出身ダミーなどを独立変数、進学した大学の入試偏差値を従属変数とする重回帰分析を行う方法である。西丸（2008）はこの手法を採用している。しかしこの手法には、大学に進学しなかった個人が分析から除外されてしまう、同一年齢層を偏りなく調査することが困難であるなどの課題がある。

もう一つの方法は、高校を単位として、中高一貫の高校とそうでない高校の難関大学進学率を比較するというものである。この手法には、高校データベースを作成すれば、母集団に対してほぼ悉皆での分析が可能になるという利点がある。もちろん、中高一貫の高校とそうでない高校では入学時点での生徒の学力水準が異なるため、入学時点での学力水準を統制して両者を比較する必要がある。本稿で用いるのはこの手法である。具体的な手順を示す。

手順１	離島・通信制を除く東京都内の全高校について、2003年中学入試偏差値、2006年高校入試偏差値、2009年難関大学進学率などを入力したデータベースを作成する。３年おきになっているのは、同一世代が分析対象となるようにするためである。また、「難関大学」は一意には定まらないが、本稿では便宜的に、旧帝国大学・東京工業大学・一橋大学合格者数に早稲田大学・慶應義塾大学・上智大学・東京理科大学・国際基督教大学合格者数の３分の１を加算した数を、高校の難関大学進学者数と定義し、その卒業生数に占める割合を難関大学進学率とした。私立大学の合格者数に３分の１を乗算するのは、私立大学の場合、合格した者が必ず進学するとは限らないからである*2。
手順２	中学入試偏差値から高校入試偏差値に対して回帰分析を行う。そして、推計された回帰式に基づき、中学入試のみ行っている高校の高校入試偏差値を予測する。これで、すべての高校について、入学時点での生徒の学力水準を一元的な指標で表すことができる。
手順３	入試偏差値（予測値を含む）から難関大学進学率に対して、曲線推定の回帰分析を行い、その残差を算出する。この残差が、入学時点での生徒の学力水準を統制した上での、その高校の難関大学進学率となる。したがって、統制済み難関大学進学率と名付ける。
手順４	統制済み難関大学進学率を従属変数、国私立一貫ダミー・国私立非一貫ダミー・専門学科ダミーなどを独立変数とする重回帰分析を行う。この分析で、国私立一貫ダミーの回帰係数が正に有意であれば、中高一貫校進学が難関大学進学を促していることになる*3。

３．使用データ

2003年中学入試偏差値は、声の教育社『平成16年度用中学受験案内』に記載されている首都圏模試センター80％合格偏差値を用いた。入試が複数回ある中学校については、第１回午前入試の偏差値を用い、共学校については、男女の偏差値の中間値を用いた。

2006年高校入試偏差値は、声の教育社『平成19年入試用東京都高校受験案内』に記載されている東京都標準50％合格偏差値を用いた。複数の学科がある高校については、定員数が最も多い学科の偏差値を用いた。

2009年難関大学合格者数は、声の教育社『平成23年度用中学受験案内』と『平成23年入試用東京都高校受験案内』に記載されている人数を用いた。浪人を含めた合格者数である*4。

2009年度卒業生数は、声の教育社『平成23年度用中学受験案内』と旺文社『2011年度高校受験案内』に記載されている人数を用いた。これらの資料に卒業生数が記載されていない３校については、当該校のホームページから卒業生数を入手した。


４．分析結果

４．１．手順１の結果
離島・通信制を除く東京都内の全高校412校について2003年中学入試偏差値、2006年高校入試偏差値、2009年難関大学進学率などを入力したデータベースを作成した。表１は学校類型ごとの難関大学進学率であり、中高一貫校において難関大学進学率が高いことが分かる。ただし、前述のように、このことから中高一貫校に進学すると難関大学に進学しやすくなるとは言えない。なぜなら、もともと学力が高い生徒が中高一貫校に進学している可能性があるからである。なお、標準偏差を見ると、中高一貫校において、難関大学進学率のばらつきが大きいことが分かる。一口に中高一貫校と言っても、その進学状況は多様である。

表１　学校類型ごとの難関大学進学率

	平均値	標準偏差	有効度数
公立（都立・区立）	0.028	0.080	170
国私立一貫	0.132	0.231	174
国私立非一貫	0.034	0.139	66
合計	0.073	0.176	410

４．２．手順２の結果
中学入試と高校入試の両方を実施している132校に対して、中学入試偏差値から高校入試偏差値への回帰分析を行った。図１に示した回帰式に基づき、中学入試のみ行っている44校の高校入試偏差値を予測する。つまり、高校入試がない高校について、「仮に高校入試があった場合の入試偏差値」を予測するということである。この時点で、学力審査を実施していないなどの理由で入試難易度が不明である高校を除く401校について、一元的な入試偏差値（生徒の入学時点での学力水準を示す指標）が得られた。

図１　中学入試偏差値から高校入試偏差値への回帰分析

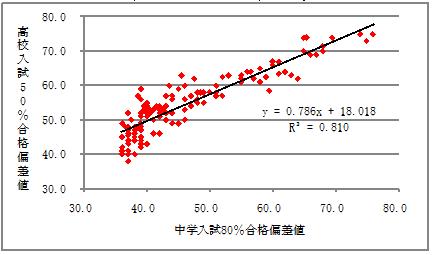
４．３．手順３の結果
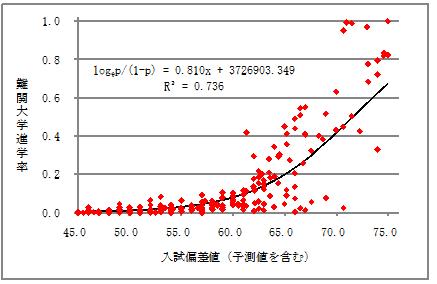
入試偏差値（手順２で得られた予測値を含む）を独立変数、難関大学進学率を従属変数として、従属変数の上限を１に設定したロジスティック曲線を当てはめた。ロジスティック曲線を当てはめた理由は、難関大学進学率は論理的に必ず０～１の値をとるからである。なお、ロジスティック変換のため、難関大学進学率pは0.99p＋0.005に変換した。

また、偏差値45未満の高校111校は難関大学進学率が０であるケースが多かったため、回帰分析に不適と判断して分析から除外した。したがって、以下の分析は「一定以上の入試難易度の高校」に関するものとなる。さらに１校は、難関大学進学率がデータ欠損しており、分析から除外される。ここで分析される学校数は289校となっている。

分析結果が図２である。この回帰分析の残差が、入学時点での生徒の学力水準を統制済みの難関大学進学率である。すなわち、この回帰曲線より上に位置している高校は「入学時点での学力に比して難関大学進学率が高い高校」であり、回帰曲線より下に位置している高校は「入学時点での学力に比して難関大学進学率が低い高校」ということになる。統制済み難関大学進学率は、難関大学進学率を指標とした場合の、その学校の教育効果とも表現できる。

図２　入試偏差値から難関大学進学率に対する回帰分析

４．４．手順４の結果
統制済み難関大学進学率を従属変数、国私立一貫ダミー・国私立非一貫ダミー・専門学科ダミーなどを独立変数とする重回帰分析の結果が表２である。

なお、理数科と英語科は専門学科ではなく普通科に含めている。主要５教科を中心にカリキュラムが組まれているという点で、専門学科より普通科に近いと考えたためである。また、早慶基附属ダミーは、早稲田大学・慶應義塾大学・国際基督教大学の附属校または系列校であること、GMARCH附属ダミーは、学習院大学・明治大学・青山学院大学・立教大学・中央大学・法政大学の附属校または系列校であることを示す。これらの変数は、大学への内部進学の影響を除いた中高一貫教育の効果を見出すために投入した。

分析の結果、どのモデルでも国私立一貫ダミーの回帰係数は統計的に有意ではない。また、有意でないだけなく、モデル２では回帰係数が負であり、モデル１とモデル３では回帰係数の値が0.005前後なので、中高一貫教育が難関大学進学率を高めるとしても、0.5％程度ということである。つまり、早稲田大学や慶應義塾大学の附属校に入学するような場合は別として、一般には、中高一貫校に進学すると難関大学に進学しやすくなるとは言えない。この分析結果は国立高校を分析から除外しても同様に得られる。

表２　統制済み難関大学進学率の規定要因（重回帰分析）
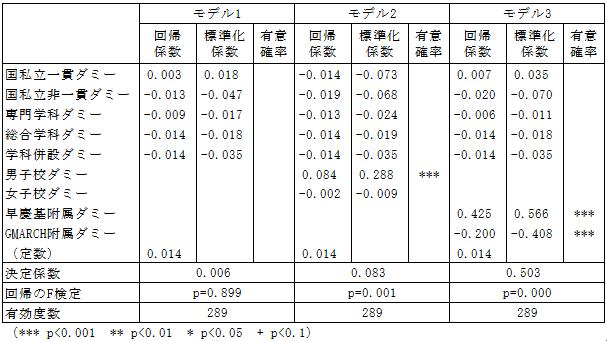なお、本稿の研究課題からは外れるが、モデル２において、男子校ダミーが正の効果を有していることは、男子校が共学校や女子校と比べて、高学歴を強く志向していることを示していると考えられる。男子校の校風によって生徒の高学歴志向が強まるのか、それとも高学歴志向が強い生徒が男子校に入学するのかは分からないが、いずれにせよ、男子校は同程度の入試難易度の共学校や女子校と比べて、難関大学に生徒を輩出しやすい。また、モデル３において、GMARCH附属ダミーが負の効果を有していることは、中堅大学の附属校に入学した生徒は、あえて難関大学進学を目指さないことを示していると考えられる。


５．結論

本稿の分析結果が示すように、中高一貫校に進学すると難関大学に進学しやすくなるという言説は正しいとは言えない。確かに、中高一貫の高校はそうでない高校と比べて難関大学進学率が高いが、その関係は入学時点での生徒の学力水準を統制すると見られなくなるのである。つまり、中高一貫教育を受けることで難関大学に進学しやすくなるというわけではない。このことはこれまでにも、石戸（1993）などによって可能性が示唆されてきたことであるが、本稿では精緻な実証分析に基づいてそれを示すことができた。

久保（2006）は、中高一貫校におけるカリキュラムが、大学受験に対応した効率的なものになっていることを示している。一方、橘木（2010）は、私立中学校・高校は公立中学校・高校と比べて教師生徒比（教師一人あたりの生徒数）が大きいことを示し、そのことが中高一貫教育の効果を引き下げている可能性を論じている*5。また、服部（1995）が指摘するような、勉学面での「中だるみ」も中高一貫校ではあり得る。これらの様々な要因が複合して、今回のような分析結果が得られたのかもしれない。

もっとも、本稿で分析した中高一貫校の効果は、あくまで難関大学進学に対する効果であって、教育効果と呼ぶべきものは他に多く存在する。それは、受験学力に回収されない、論理的思考力やコミュニケーション能力の育成であったり、生徒の日々の学校生活に対する充足感であったりするだろう。たとえば、須藤（2011）では、私立上位校において、生徒の学校満足度が非常に高いことなどが示されている。したがって、本稿の知見のみに基づいて、中高一貫教育の効果全般を論じることは適切ではない。今後は、難関大学進学以外の要素に対する、中高一貫教育の効果を検証することが求められる。


-------------------------------------------------------

＜注＞
*1 　2008年度「東京大学学生生活実態調査」から算出した。なお、国立高校は必ずしもすべてが中高一貫校ではないことには注意が必要である。
*2 　３分の１という判断が適切であるという証明はできない。しかし、試みに２分の１で算出したところ、難関大学進学者数が卒業生数を超える高校が複数現れたため、少なくとも２分の１を用いることは不適切であると考えられる。なお、早稲田大学・慶應義塾大学・国際基督教大学の附属校または系列校から同大学への合格者はほぼ100％進学するため、合格者数に３分の１を乗算するという処理は行わなかった。
*3 　2003年中学入試の時点で、公立（都立・区立）の中高一貫校は存在しないため、本データベースにおける中高一貫校はすべて国立・私立の中高一貫校である。
*4 　中高一貫校の大学合格者数の中の中学入学生と高校入学生の内訳が不明であり、両者を識別できないことは、本データの限界である。つまり、本稿で分析されるのは、中高一貫教育が「高校入学生まで含めたその学校の難関大学進学率」に与える影響ということになる。
*5 　教師生徒比は「学校基本調査」に基づいて算出されており、公立中学校は14.3、私立中学校は18.1、公立高校は13.0、私立高校は17.4となっている。

＜参考文献＞
石戸教嗣 1993「教育における『公』と『私』‐その理念的考察」『教育社会学研究』第52集 東洋館出版社 pp.5-19.
井上修 2001『私立中高一貫校しかない！‐教育階層化時代の勝ちぬき方』宝島社。
旺文社編 2010『2011年度高校受験案内』旺文社。
久保良宏 2006「中高一貫教育校における数学科のカリキュラムに関する研究」『日本数学教育学会誌』第88集9号 日本数学教育学会 pp.2-10.
声の教育社編集部 2003『平成16年度用中学受験案内』声の教育社。
声の教育社編集部 2006『平成19年入試用東京都高校受験案内』声の教育社。
声の教育社編集部 2010『平成23年度用中学受験案内』声の教育社。
声の教育社編集部 2010『平成23年入試用東京都高校受験案内』声の教育社。
須藤康介 2011「私立中高一貫校の学校階層構造‐マクロ・ミクロデータの分析から」『学校教育研究』第26号 教育開発研究所 pp.99-111.
橘木俊詔 2010『日本の教育格差』岩波新書。
東京大学学内広報 2009「2008年（第58回）学生生活実態調査の結果」（http://www.u-tokyo.ac.jp/gen03/kouhou/1393/pdf/1393.pdf）。
西丸良一 2008「大学進学におよぼす国・私立中学校進学の影響」『教育学研究』第75巻1号 日本教育学会 pp.24-33.
服部泰秀 1995「私学の特色ある一貫教育に関する調査・研究‐教育効果の面よりみた中高一貫教育充実に関する研究」『日本私学教育研究所紀要』第30巻第1号 日本私学教育研究所 pp.191-209.
和田秀樹 2008『子どもは公立に預けるな！』ソフトバンク新書。